Breakdown of the Right Hand Rule Again

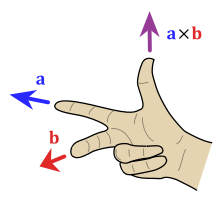
Mnemonic for agreement orientation of vectors in 3D space

Finding the management of the cross product by the right-hand rule

In mathematics and physics, the correct-manus rule is a common mnemonic for agreement orientation of axes in iii-dimensional space.

Most of the various left-hand and correct-hand rules arise from the fact that the three axes of three-dimensional space accept ii possible orientations. I tin meet this by holding ane's hands outward and together, palms upwards, with the fingers curled, and the thumb out-stretched. The gyre of the fingers represents a movement from the commencement (x axis) to the second (y axis), then the tertiary (z axis) can point forth either thumb. Left-hand and correct-hand rules ascend when dealing with coordinate axes. The rule can be used to find the direction of the magnetic field, rotation, spirals, electromagnetic fields, mirror images, and enantiomers in mathematics and chemical science.

The sequence is often: index finger, then middle, and then thumb. Nevertheless, two other sequences also piece of work because they preserve the cycle:

Centre finger, and so pollex, then index finger.
Thumb, then index finger, and then middle (e.one thousand., see the ninth serial of the Swiss 200-francs banknote).

Curve orientation and normal vectors [edit]

In vector calculus, it is often necessary to relate the normal to a surface to the bend bounding it. For a positively-oriented curve $C$ bounding a surface $S$ , the normal to the surface $n̂$ is defined such that the right thumb points in the management of $n̂$ , and the fingers roll along the orientation of the bounding curve $C$ .

Correct-hand rule for curve orientation.

Coordinates [edit]

Left-handed coordinates on the left,
right-handed coordinates on the right.

For right-handed coordinates use right hand.
For left-handed coordinates use left hand.
Axis or vector	2 fingers and thumb	Curled fingers
x, 1, or A	First or alphabetize	Fingers extended
y, ii, or B	Second finger or palm	Fingers curled 90°
z, iii, or C	Pollex	Thumb

Coordinates are ordinarily right-handed.

For right-handed coordinates the correct thumb points forth the z axis in the positive direction and the ringlet of the fingers represents a movement from the first or x axis to the 2nd or y axis. When viewed from the superlative or z axis the system is counter-clockwise.

For left-handed coordinates the left pollex points along the z axis in the positive direction and the curled fingers of the left hand represent a motion from the beginning or ten axis to the second or y axis. When viewed from the top or z axis the system is clockwise.

Interchanging the labels of whatever ii axes reverses the handedness. Reversing the direction of i axis (or of all iii axes) besides reverses the handedness. (If the axes do non accept a positive or negative direction and then handedness has no pregnant.) Reversing two axes amounts to a 180° rotation effectually the remaining axis.^[1]

Rotations [edit]

A rotating body [edit]

Conventional direction of the axis of a rotating body

In mathematics, a rotating torso is commonly represented by a pseudovector forth the axis of rotation. The length of the vector gives the speed of rotation and the direction of the axis gives the direction of rotation according to the right-hand rule: correct fingers curled in the direction of rotation and the correct thumb pointing in the positive direction of the axis. This allows some easy calculations using the vector cross product. No part of the body is moving in the direction of the axis arrow. By coincidence, if the thumb is pointing due north, Earth rotates in a prograde management according to the right-hand rule. This causes the Sun, Moon, and stars to appear to revolve westward according to the left-hand rule.

Helices and screws [edit]

Left- and right-handed screws

A helix is a curved line formed past a point rotating around a center while the eye moves upward or down the z axis. Helices are either correct- or left-handed, curled fingers giving the direction of rotation and thumb giving the management of advance along the z centrality.

The threads of a screw are a helix and therefore screws tin can be right- or left-handed. The rule is this: if a screw is right-handed (about screws are) betoken your correct pollex in the management you want the screw to go and plough the spiral in the direction of your curled right fingers.

Electromagnetism [edit]

When electricity (conventional electric current) flows in a long straight wire it creates a circular or cylindrical magnetic field effectually the wire according to the right-hand dominion. The conventional current, which is the opposite of the actual flow of electrons, is a flow of positive charges forth the positive z axis. The conventional direction of a magnetic line is given by a compass needle.
Electromagnet: The magnetic field around a wire is quite weak. If the wire is coiled into a helix all the field lines inside the helix point in the same direction and each successive coil reinforces the others. The accelerate of the helix, the non-circular role of the current and the field lines all point in the positive z management. Since there is no magnetic monopole, the field lines leave the +z end, loop effectually outside the helix, and reenter at the −z end. The +z end where the lines exit is defined as the north pole. If the fingers of the right paw are curled in the direction of the circular component of the electric current, the right thumb points to the north pole.
Lorentz force: If a positive electrical charge moves across a magnetic field it experiences a force co-ordinate Lorentz force, with the direction given past the correct-hand rule. If the curl of the right fingers represents a rotation from the direction the charge is moving to the direction of the magnetic field so the forcefulness is in the management of the right thumb. Because the accuse is moving, the forcefulness causes the particle path to bend. The bending strength is computed by the vector cross product. This means that the bending force increases with the velocity of the particle and the strength of the magnetic field. The forcefulness is maximum when the particle direction and magnetic fields are at right angles, is less at any other bending and is cipher when the particle moves parallel to the field.

Ampère's correct-hand grip rule [edit]

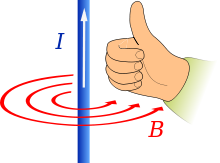
Prediction of management of field (B), given that the current I flows in the direction of the thumb

Finding direction of magnetic field (B) for an electrical coil

Ampère's correct-hand grip rule^[ii] (besides called correct-hand screw rule, coffee-mug rule or the corkscrew-rule) is used either when a vector (such as the Euler vector) must be divers to represent the rotation of a body, a magnetic field, or a fluid, or vice versa, when information technology is necessary to define a rotation vector to understand how rotation occurs. It reveals a connection between the current and the magnetic field lines in the magnetic field that the current created.

André-Marie Ampère, a French physicist and mathematician, for whom the rule was named, was inspired past Hans Christian Ørsted, some other physicist who experimented with magnet needles. Ørsted observed that the needles swirled when in the proximity of an electric current-carrying wire, and concluded that electricity could create magnetic fields.

Awarding [edit]

This dominion is used in two different applications of Ampère'due south circuital law:

An electrical current passes through a straight wire. When the thumb is pointed in the direction of conventional current (from positive to negative), the curled fingers will then point in the management of the magnetic flux lines effectually the conductor. The direction of the magnetic field (counterclockwise instead of clockwise when viewing the tip of the pollex) is a result of this convention and non an underlying physical phenomenon.
An electric current passes through a solenoid, resulting in a magnetic field. When wrapping the right hand around the solenoid with the fingers in the direction of the conventional current, the thumb points in the direction of the magnetic due north pole.

Cantankerous products [edit]

The cross product of ii vectors is oft taken in physics and engineering science. For example, in statics and dynamics, torque is the cross product of lever length and forcefulness, while athwart momentum is the cross product of distance and linear momentum. In electricity and magnetism, the force exerted on a moving charged particle when moving in a magnetic field B is given by:

\mathbf {F} =q\mathbf {v} \times \mathbf {B}

The direction of the cross production may be constitute past application of the right hand rule as follows:

The alphabetize finger points in the management of the velocity vector v.
The centre finger points in the direction of the magnetic field vector B.
The thumb points in the direction of the cantankerous production F.

For example, for a positively charged particle moving to the north, in a region where the magnetic field points west, the resultant strength points upwards.^[one]

Applications [edit]

The right-hand rule is in widespread use in physics. A list of concrete quantities whose directions are related past the right-hand rule is given beneath. (Some of these are related only indirectly to cross products, and use the second grade.)

For a rotating object, if the right-manus fingers follow the curve of a betoken on the object, then the thumb points along the axis of rotation in the direction of the angular velocity vector.
A torque, the force that causes it, and the position of the betoken of awarding of the force.
A magnetic field, the position of the point where it is determined, and the electric current (or change in electrical flux) that causes information technology.
A magnetic field in a roll of wire and the electric current in the wire.
The force of a magnetic field on a charged particle, the magnetic field itself, and the velocity of the object.
The vorticity at whatsoever indicate in the field of flow of a fluid
The induced electric current from motion in a magnetic field (known as Fleming's right-mitt dominion).
The x, y and z unit of measurement vectors in a Cartesian coordinate system tin can exist chosen to follow the right-manus rule. Right-handed coordinate systems are often used in rigid body and kinematics.

Encounter besides [edit]

Chirality (mathematics)
Curl (mathematics)
Fleming's left-hand rule for motors
Improper rotation
ISO 2
Oersted's law
Poynting vector
Pseudovector
Reflection (mathematics)

References [edit]

^ ^a ^b Watson, George (1998). "PHYS345 Introduction to the Right Hand Rule". udel.edu. University of Delaware.
^ IIT Foundation Series: Physics – Class 8, Pearson, 2009, p. 312.

External links [edit]

Right and Left Manus Rules - Interactive Coffee Tutorial National High Magnetic Field Laboratory
A demonstration of the right-manus rule at physics.syr.edu
Weisstein, Eric Due west. "Right-manus rule". MathWorld.
Dr. Johannes Heidenhain : Right Mitt Rule - Heidenhain TNC Preparation : heidenhain.de
Christian Moser : right-manus-rule : wpftutorial.net

williamsshave1981.blogspot.com

Source: https://en.wikipedia.org/wiki/Right-hand_rule